

Jean-Marc Alliot — Thomas Schiex
Les jeux, activité futile en apparence, ont toujours fasciné les informaticiens1. Ainsi, Babbage2 avait envisagé de programmer sa machine analytique pour jouer aux échecs, Claude Shannon3 décrivit en 1950 les rudiments d’un programme d’échecs, comme le fit également Alan Mathison Turing. Dès les débuts de l’IA, les premiers chercheurs se lancèrent dans la réalisation de programme de jeux4. Ainsi, un des tous premiers programmes de Simon, Newell, Shaw fut un programme de jeux d’échecs et Arthur Samuel écrivit dans les années 50 un programme de jeu de dames américaines.
Pourquoi cette fascination des informaticiens pour le domaine des jeux ? Tout d’abord parce qu’il semble intuitivement (et inconsciemment) que la pratique de jeux intellectuels soit le propre de l’homme. De plus, tout jeu apparaît un peu comme un champ clos de tournoi au Moyen Âge : chacun est astreint à respecter des règles strictes et précises, et ne peut l’emporter que grâce à sa valeur et à son habileté. La victoire et la défaite sont sanctionnées clairement et sans appel possible. Réaliser une machine qui joue aussi bien qu’un homme, voire mieux, << prouverait >> l’intelligence (ou la supériorité) des ordinateurs, et serait apparue comme une grande réussite pour l’IA, du moins à ses débuts.
Enfin, comme le dit Donald Michie :
<< La recherche sur le jeu d’échecs est le champ le plus important de la recherche cognitive5. Les échecs seront pour nous ce que la drosophile6 a été pour les généticiens : un moyen simple et pratique de développer de nouvelles techniques. >>
Sur le plan technique, le domaine des jeux est très << spécifiable >> au sens informatique du terme : les règles sont généralement simples, et surtout les interactions avec le monde extérieur parfaitement nulles : il s’agit d’un micro-monde totalement clos, et donc aisément accessible (en apparence) à un programme d’ordinateur. D’autre part, les informaticiens pensaient (plus perfidement) que sa puissance de calcul devrait donner, dans un univers aussi restreint, un avantage considérable à l’ordinateur.
Les choses ne se passèrent pas aussi facilement. Il fallut rapidement distinguer les jeux très simples (morpion) où une analyse exhaustive est possible, des jeux plus complexes comme les dames ou les échecs qui demandent des algorithmes spécifiques et des méthodes heuristiques de recherche, ou encore des jeux à information partielle comme le bridge ou le poker qui demandent en plus des raisonnements de type probabiliste.
Nous allons dans ce chapitre faire un tour d’horizon des techniques de programmation des jeux, et examinerons en détail trois exemples : Othello, les échecs et le bridge. Ces exemples nous permettront d’introduire quelques principes supplémentaires importants de la théorie moderne de la programmation des jeux.
Les joueurs (surtout d’échecs) ayant été des sujets d’études pour les psychologues, nous présenterons quelques-uns des résultats les plus intéressants, résultats qui sont d’autant plus significatifs qu’ils dégagent des facteurs communs à presque toutes les activités humaines.
Les programmes de jeux à deux joueurs et à information totale utilisent des techniques de représentation semblables à celles que nous avons vues dans le paragraphe précédent : espace d’états et arbres ou graphes. On utilise également des systèmes de production pour générer les états. En revanche, du fait de la présence de deux joueurs ayant des objectifs antagonistes (et non plus identiques), la recherche dans ces arbres7 ne peut se faire en recourant à des algorithmes du type A*.
La méthode générale utilisée pour ces jeux est la suivante : à partir d’une position (ou état) donnée, on génère l’ensemble des positions (ou états) que l’ordinateur peut atteindre en jouant un coup (niveau 1 de profondeur). À partir de chacune de ces positions du niveau 1, on génère l’ensemble des positions que l’adversaire peut à son tour atteindre (niveau 2). On peut alors recommencer l’opération aussi longtemps que le permet la puissance de calcul de l’ordinateur et générer les niveaux 3, 4, …, n. On construit ainsi un arbre de l’espace d’états du problème. Il est clair qu’il est impossible, dans la plupart des jeux, de générer l’ensemble de l’espace d’états du problème. Ainsi, aux échecs, le facteur de branchement8 est environ de 35 à chaque niveau de profondeur. Une partie d’échecs convenablement jouée devant contenir au moins une trentaine de demi-coups, le nombre d’états de l’espace d’états est alors de l’ordre de 3530=20991396429661901749543146230280399322509765625 : même l’ordinateur le plus puissant du monde ne pourrait le générer en un temps raisonnable (inférieur à l’âge de l’univers par exemple). On doit donc limiter l’exploration à une profondeur maximale de résolution. Lorsqu’on a atteint cette profondeur, l’ordinateur attribue à chacune des feuilles une valeur par l’intermédiaire d’une fonction d’évaluation. Cette valeur correspond à l’estimation de la position. Cette estimation peut se faire du point de vue d’un joueur fixe (convention minimax) ou du joueur qui a le trait à cette profondeur (convention négamax). Il doit alors, à partir du niveau 0 (la racine), jouer le coup de niveau 1 qui lui garantit le gain maximal contre toute défense de son adversaire, en supposant que celui-ci utilise également une stratégie optimale, c’est-à-dire qu’il joue lui-même à chaque coup le gain qui lui garantit le gain maximal contre toute défense. Ce mécanisme est appelé principe minimax9.
Nous allons détailler les deux phases principales de la résolution : la fonction d’évaluation des états terminaux et les algorithmes de recherche.
La fonction d’évaluation tente d’associer à une position une valeur estimant la qualité de la position pour un des deux joueurs. Les fonctions d’évaluation furent étudiées très tôt. Les premières proposées furent évidemment les plus simples. Aux dames par exemple, on peut effectuer la différence entre le nombre de ses pions et le nombre de pions de l’adversaire. Il est clair qu’une fonction heuristique élaborée permet de mieux jouer : si j’inclus dans ma fonction d’évaluation des notions d’attaque et de défense de pions, j’améliore mon niveau de jeu. En revanche, plus la fonction est élaborée et plus il faut de temps pour la calculer, ce qui limitera la profondeur d’exploration de l’arbre. Nous examinerons plus en détail les fonctions d’évaluation en étudiant la programmation des échecs et d’Othello.
L’algorithme minimax10 est un algorithme de type exploration en profondeur d’abord comme nous les avons décrits au chapitre précédent. Il implante le principe minimax que nous avons évoqué. Le jeu comporte deux joueurs : O (l’ordinateur) et H (son adversaire). Une fonction d’évaluation h est chargée d’évaluer la qualité d’une position de jeu terminale (position de profondeur maximale ou sans descendance) du point de vue de O (par exemple). À chaque niveau où O a le trait, il peut choisir son coup et choisira donc celui de valeur maximale pour lui, on parle de nœud de type Max et du joueur Max. À chaque niveau où H a le trait, O va supposer que l’adversaire essaie de le mettre en mauvaise posture (minimiser ses gains) et choisira donc le coup de valeur minimale pour O (nœud de type Min, joueur Min). Ce n’est que sur les feuilles que l’on peut directement appliquer la fonction d’évaluation h. Sinon, on s’appuie sur une écriture récursive. L’algorithme, qui travaille en profondeur d’abord et jusqu’à la profondeur n, ne stocke jamais plus de n positions à la fois. En effet, il commence par générer une branche complète. Il évalue alors la feuille terminale et marque le sommet n−1 avec cette valeur. Il repart alors de la position de niveau n−1 et génère la feuille suivante (niveau n). Il utilise l’évaluation de cette feuille pour modifier le marquage du niveau n−1, et répète l’opération jusqu’à ce qu’il ait généré toutes les feuilles de niveau n issues de cette position de niveau n−1. Il utilise alors la valeur de ce niveau n−1 pour marquer le niveau n−2, remonte à la position du niveau n−2 et génère la position de niveau n−1 suivante, et continue le processus jusqu’à ce que toutes les feuilles et tous les niveaux aient été générés.
Une convention simplificatrice (du moins pour le programmeur) consiste à considérer qu’on évalue la qualité d’une position non pas du point de vue d’un joueur fixe donné (joueur racine) mais du point de vue du joueur qui a le trait sur cette position. La fonction heuristique doit évidemment être modifiée en conséquence. Dans tous les cas, que ce soit O ou H qui ait le trait, le raisonnement sera le même : pour évaluer le mérite d’un nœud du point de vue du joueur qui a le trait, en connaissant le mérite des positions filles (du point de vue de l’adversaire, qui a le trait sur ces positions), on considère le coup qui maximise (car on veut gagner) l’opposé des mérites des positions filles (car elles ont été évaluées par l’adversaire). Dans tous les cas, la valeur d’un nœud est simplement le maximum des opposés de la valeur des fils. L’écriture de la fonction récursive s’en voit simplifiée. On parle de convention négamax.
Un exemple de parcours par un algorithme minimax est fourni sur la figure 1.1.
On constate que l’algorithme minimax doit complètement décrire l’arbre pour fournir une solution, ce qui, on le verra, est souvent excessif. L’algorithme alpha-beta11 est une amélioration de l’algorithme minimax qui réalise un élagage de certaines branches qu’il est inutile de visiter.
Examinons l’arbre de la figure 1.2, alors que l’algorithme minimax a déjà parcouru les deux premières branches de la racine, et va s’engager dans la troisième et dernière branche. On sait alors que la racine a une valeur au moins égale à 3 puisqu’un des nœuds fils a déjà été évalué à 3 et que le nœud racine est de type Max. Lorsque, durant l’exploration de la troisième branche, on évalue la première feuille, celle-ci retourne la valeur 1. Son père, qui est un nœud Min, ne va pas pouvoir dépasser la valeur 1, ceci quelles que puissent être les valeurs des deux fils encore inexplorés. Or, pour modifier la valeur de la racine, et donc le coup à jouer, il faudrait que ce nœud dépasse la valeur 3, puisque la racine est de type Max. Les deux feuilles restantes sont donc inintéressantes et ne seront pas explorées par alpha-beta .
De façon plus synthétique, lorsque dans le parcours de l’arbre de jeu par minimax il y a remise en cause de la valeur d’un nœud, si cette valeur atteint un certain seuil, il devient inutile d’explorer la descendance encore inexplorée de ce nœud.
Il y a en fait deux seuils, appelés pour des raisons historiques, alpha (pour les nœuds Min) et beta (pour les Max) :
Ceci nous amène à l’énoncé de l’algorithme alpha-beta qui maintient ces deux valeurs durant le parcours de l’arbre (cf. Algorithme ??). Lors de son utilisation, on l’appellera par AlphaBeta(Racine,−∞,+∞).

Une définition beaucoup plus concise, mais peut-être moins intuitive, peut être obtenue en utilisant la convention négamax ; il devient alors inutile de distinguer les nœuds Min des nœuds Max (cf. Algorithme ??). Cet algorithme calcule alors la valeur négamax de la racine qui est, au signe près, égale à sa valeur minimax.
L’algorithme est d’autant plus efficace que l’on parcourt l’arbre << de la bonne façon >>. Quand le niveau est maximisant, il faut examiner d’abord les coups qui ont le plus de chance de générer des positions à forte valeur d’évaluation et réciproquement. Nous verrons dans la suite de ce chapitre comment réaliser de tels mécanismes. Si l’arbre est parcouru exactement dans le bon ordre, le nombre de feuilles examinées est environ 2 √N où N est le nombre de feuilles total de l’arbre, alors que l’algorithme minimax examine, lui, les N feuilles.
Il s’agit d’un algorithme relativement peu connu, en tous cas nettement moins connu que l’algorithme alpha-beta . Il a pourtant été démontré qu’il lui est théoriquement supérieur12, dans le sens où il n’évaluera pas un nœud si alpha-beta ne l’examine pas, tout en élaguant éventuellement quelques branches explorées par alpha-beta . Cette qualité supplémentaire se paie, SSS étant un gros consommateur de mémoire. [Stratégie] Étant donné un arbre de jeu J, on appelle stratégie ou sous-arbre solution pour le joueur Max , un sous-arbre de J qui :
Une stratégie indique au joueur Max ce qu’il doit jouer dans tous les cas. S’il s’agit d’un nœud Max , il a toute liberté de choix et jouera donc le coup indiqué par la stratégie. Si c’est un nœud Min, la stratégie contient tous ses fils et envisage donc toutes les réponses éventuelles de l’adversaire. Si Max respecte une stratégie, il est assuré d’aboutir à une des feuilles de la stratégie. Si l’on se place dans le cas habituel où l’arbre de jeu est développé jusqu’à une profondeur n, le mérite des positions terminales étant estimé par une fonction d’évaluation, la valeur d’une stratégie pour Max est donc le minimum des valeurs des feuilles de cette stratégie, gain assuré contre toute défense de Min. Le but de SSS est d’exhiber la stratégie de valeur maximum pour Max . Sa valeur sera, par définition, la valeur minimax de l’arbre J. [Stratégie partielle] Étant donné un arbre de jeu J, on appelle stratégie partielle pour le joueur Max , un sous-arbre de J qui:
Une stratégie partielle P représente implicitement l’ensemble des stratégies complètes auxquelles on peut aboutir en développant P via :
Toutes les stratégies complètes représentées par une stratégie partielle partagent les nœuds de la stratégie partielle, et en particulier, elles partagent les nœuds terminaux sur lesquels on a appliqué la fonction d’évaluation. La valeur d’une stratégie étant égale au minimum de la valeur de ses feuilles, la valeur d’une stratégie partielle constitue une borne supérieure (i.e., une estimation optimiste) de la valeur des stratégies complètes qu’elle représente.
L’algorithme SSS explore un espace d’état dont chaque nœud est une stratégie partielle, en utilisant une approche meilleur d’abord avec une heuristique minorante qui sera la valeur des stratégies partielles et qui garantit l’optimalité. Il ajoute un raffinement permettant d’éviter le développement de certaines stratégies partielles dont on peut démontrer l’absence d’intérêt.
Figure 1.3: SSS et arbre de jeu
Considérons par exemple l’arbre de jeux de la figure 1.3 et appliquons un meilleur d’abord avec une heuristique égale à la valeur des stratégies partielles (valeur de +∞ si la stratégie ne contient pas de nœud terminal). Dans la suite, nous décrirons une stratégie partielle par un couple formé de l’ensemble des nœuds qu’elle contient et de sa valeur estimée. Nous désignerons par G la liste des stratégies partielles.
L’algorithme du SSS s’inspire de cette remarque. À partir du moment où une sous-stratégie optimale est établie (comme au point (6)), la stratégie optimale est marquée, et toutes les sous-stratégies sous-optimales supprimées de G. En voici la description précise. Nous noterons :
On dira qu’un nœud est résolu, si la stratégie complète issue de ce nœud a été déterminée. Un nœud qui n’est pas résolu est vivant. Il ne faut pas confondre par la suite nœud (lié à l’arbre de jeu) et état (lié à l’arbre d’exploration des stratégies).

L’algorithme (cf. Algorithme ??) traite le meilleur état courant (n,t,e) selon son type. Si l’état est marqué vivant, cela signifie que la meilleure stratégie issue du nœud correspondanten n’est pas encore encore connue et il faut continuer à la developper :
Si l’état (n,t,e) est marqué résolu, une stratégie complète optimale issue du nœud est connue et il faut faire remonter l’information :
Comme nous l’annoncions initialement, l’algorithme du SSS est supérieur à alpha-betafootnoteIl faut pour cela que les deux algorithmes développent le même arbre, dans un ordre comparable. Ceci nécessite, dans le cas de l’insertion dans G de deux nœuds de même valeur, de mettre en première position le nœud exploré en premier par alpha-beta et entraîne l’emploi de finesse de programmation (ordonnancement fixe des nœuds…) qu’il est inutile de pratiquer lorsqu’on désire employer SSS pour autre chose qu’une comparaison à alpha-beta .. Récemment, un algorithme paramétrable sur la quantité de mémoire (longueur maximum de la liste G) qu’il peut utiliser — l’IterSSS* — a été exhibé [BB86]. Il permet d’obtenir des performances variant entre celles d’alpha-beta (mémoire minimum) et de SSS (mémoire suffisamment importante). Le tableau suivant indique les performances de cet algorithme en pourcentage de nœuds visités sur différents arbres uniformes de facteurs de branchements et de profondeurs variables :
| Profondeur | Branchement | alpha-beta | SSS | longueur G | IterSSS |
| 15 | 2 | 12,47 | 8,5 | 9 | 12,4 |
| 64 | 10,36 | ||||
| 192 | 9,37 | ||||
| 256 | 8,5 | ||||
| 6 | 5 | 16,51 | 11,48 | 13 | 15,49 |
| 63 | 12,68 | ||||
| 95 | 12,6 | ||||
| 125 | 11,48 | ||||
| 10 | 3 | 10,44 | 6,44 | 11 | 10,11 |
| 122 | 7,75 | ||||
| 243 | 6,44 |
Nous décrirons rapidement l’algorithme Scout , élaboré par J. Pearl [Pea90] comme outil théorique. Son efficacité est, en général, inférieure à celle d’alpha-beta , pour une consommation mémoire du même ordre. Il peut toutefois lui être supérieur.
Scout repose sur une idée fort simple : si l’on disposait d’un moyen efficace pour comparer (sans nécessairement la déterminer) la valeur minimax d’un nœud à une valeur donnée, une quantité importante de recherche pourrait être évitée. Considérons par exemple un nœud Max n, ayant deux fils : f1, dont la valeur ν est connue, et f2. Si l’on sait que la valeur de f2 est inférieure à ν, il est inutile d’explorer la branche de f2.
Scout s’appuie donc sur deux procédures simples : la première, appelée Test permet de vérifier si la valeur d’un nœud n est strictement supérieure (ou supérieure ou égale) à une valeur donnée v. Nous continuerons à désigner par h la fonction heuristique.

La seconde, Eval, utilise Test et applique le principe donné plus haut pour calculer la valeur minimax d’un arbre de jeu. Elle prend en paramètre un nœud n.

Il pourrait sembler que, du fait de la redondance éventuelle des évaluations, lorsque ScoutTest ne permet pas la coupure, Scout devrait être très inférieur à alpha-beta, voire même à minimax. Une étude mathématique du comportement asymptotique de Scout montre un comportement identique à alpha-beta pour des profondeurs élevées. Dans le cas de certains jeux (jeu de Kalah), il peut même lui être supérieur (jusqu’à 40% d’amélioration à profondeur 5). Bien qu’aucune preuve ne vienne l’appuyer, il semble que Scout soit plus particulièrement adapté aux arbres profonds, ayant un facteur de branchement faible14.
Le tableau suivant reprend l’ensemble des algorithmes de jeu présentés (minimax, alpha-beta , SSS , Scout ) et indique les performances relatives de chacun d’eux,
sur le jeu de l’Othello pour différentes profondeurs p.
| p | minimax | Scout | alpha-beta | SSS |
| 1 | 3 – 0,37 | 4 – 0,45 | 3 – 0,36 | 3 – 0,36 |
| 2 | 14 – 1,38 | 21 – 2.09 | 13 – 1,4 | 11 – 1,19 |
| 3 | 61 – 6,0 | 45 – 5,0 | 37 – 3,9 | 35 – 3,7 |
| 4 | 349 – 32,5 | 246 – 23,7 | 150 – 14,77 | 95 – 10,0 |
| 5 | 2050 – 185,7 | 615 – 61,6 | 418 – 41,4 | 292 – 19,2 |
| 6 | 13773 – 1213,5 | 2680 – 254,5 | 1830 – 172,9 | 1617 – 117,3 |
On notera les mauvaises performances de Scout à faible profondeur (plus mauvais que le simple minimax) et la nette supériorité de SSS . Il faut cependant noter que nous n’avons pu poursuivre les tests avec SSS au-delà de la profondeur 6 pour des raisons de place mémoire.
Les différents algorithmes et résultats présentés ci-dessus sont parfaitement intéressants mais ne sont plus utilisés aujourd’hui sous cette forme. De nombreuses améliorations ont été apportées et il est indispensable de les connaitre pour espérer écrire un programme performant.
On doit dans la pratique s’intéresser au système de contrôle du temps. Le programme dispose d’un temps total pour jouer l’ensemble de la partie. Il serait possible d’implanter deux techniques pour que l’ordinateur ne consomme pas trop de temps sur un coup. On pourrait tout d’abord accorder un temps donné pour jouer le coup et estimer la profondeur maximale que l’on peut atteindre sans dépasser ce temps. Cette solution présente un inconvénient : il est très difficile de trouver une fonction qui estime le temps que prendra un calcul à une profondeur donnée. On risque de se retrouver en dépassement de temps. On préfère donc utiliser une méthode un peu différente. On fait fonctionner l’algorithme alpha-beta à un niveau minimal (3 par exemple). On compare le temps utilisé avec le temps disponible. S’il reste du temps, on relance la recherche au niveau 4, puis au niveau 5…Cette méthode (habituellement référencée sous le nom de Depth First Iterative Deepening [Kor85, SA78, MS90]) présente un autre avantage. On constate aisément qu’un algorithme alpha-beta est d’autant plus efficace qu’il évalue en premier les meilleurs coups. On profite donc du résultat de la recherche à la profondeur n pour classer les coups et faire examiner en premier au programme les meilleurs coups de la profondeur n lorsqu’il effectue la recherche en profondeur n+1.
Le principe des tables de transposition est le suivant : pour chaque position rencontrée dans la recherche, l’algorithme minimax retourne une évaluation. Il s’agit de conserver dans une table la valeur de chacune des positions rencontrées de façon à pouvoir réutiliser directement cette valeur lors des recherches suivantes. Les informations stockées pour une position sont représentées sur la figure 1.4.
position évaluation meilleur distance à la coup position terminale
Nous allons voir cela sur un exemple pratique. Soit l’arbre minimax représenté sur la figure 1.5. Les informations stockées pour la position P1 sont représentées figure 1.6.
position évaluation meilleur distance à la coup position terminale P1 20 Gauche 2
Figure 1.6: Valeurs stockées pour la position P1 de l’arbre minimax représenté sur la figure précédente
Supposons que dans une recherche future l’ordinateur rencontre à nouveau la position P1. Si la distance à la racine de P1 est plus grande dans la table de transposition que dans la recherche actuelle, l’ordinateur ne poursuivra pas l’évaluation : il se contentera de recopier la valeur stockée dans la table de transposition. En revanche, si la distance à la racine est plus petite dans la table de transposition que dans l’évaluation courante, le programme terminera normalement l’évaluation de la position et remplacera l’ancienne évaluation de la table de transposition par celle qu’il aura calculée, puis stockera la nouvelle valeur de la distance à la racine.
Si les tables de transposition fonctionnaient suivant ce principe, un problème se poserait rapidement : comment stocker tous les éléments de la table de transposition (et en particulier la position de chacune des pièces sur l’échiquier) dans la mémoire du calculateur, et comment retrouver rapidement une position. On utilise une structure de données connue sous le nom de table de hachage16 ; au lieu d’utiliser la position en entier pour retrouver la valeur de cette position, on utilise un nombre qui caractérise cette position. Nous allons examiner brièvement sur un exemple une méthode permettant de construire ce nombre pour une position aux échecs.
On construit une table contenant, pour chaque pièce de chaque couleur sur chacune des cases de l’échiquier, un nombre binaire de 32 chiffres choisi de façon aléatoire (voir exemple table 1.1). Pour une position donnée, on construit alors le code de hachage en faisant un << ou-exclusif17 >> entre chacune des valeurs associée à chacune des pièces. Ainsi, pour la position représentée sur la figure 1.7, la valeur sera :
| Tour blanche en a1 | 10101011110110110101010110101101 | ⊕ |
| Roi blanc en e1 | 11010110101001001010001011010110 | ⊕ |
| Roi noir en e8 | 00100101010110110100100010101000 | = |
| 01011000001001001011111111010011 |
Le grand intérêt de cette méthode est qu’elle permet de calculer la valeur de hachage d’une position après déplacement d’une pièce, simplement en ajoutant à la valeur de hachage de la position originale le code de la pièce sur la nouvelle case et le code de la pièce sur l’ancienne case. C’est une propriété du << ou-exclusif >>.
Un des problèmes des tables de hachage est que rien ne nous garantit que deux positions différentes ne vont pas avoir la même valeur de hachage, ce qui risquerait de nous amener à des conclusions fausses sur la valeur d’une position. Cette probabilité de collision est d’autant plus faible que la taille de la table est importante.
Il reste maintenant à stocker un élément de la table de hachage. On ne peut utiliser la valeur de hachage comme index de tableau car elle est généralement trop grande (un tableau avec un index sur 32 bits occuperait quatre milliards de positions mémoire, ce qui est déraisonnable). On peut par exemple utiliser les 16 premiers bits de la valeur de hachage comme index du tableau. On prend alors le risque que des positions aient des valeurs de hachage différentes et le même index. Il y a alors conflit. Il existe différentes méthodes pour gérer ce type de problème, la plus simple étant de remplacer la plus ancienne des deux valeurs par la plus récente18.
La méthode des tables de transposition permet d’améliorer de façon spectaculaire la vitesse de recherche d’un calculateur, car elles permettent l’implantation de la version la plus classiquement utilisée de l’alpha-beta , l’alpha-beta avec mémoire. Sa structure est un petit peu plus complexe que celle de l’alpha-beta standard, car il fait appel aux tables de transposition pour stocker les bornes supérieures et inférieurs des positions déjà évaluées. Nous le présentons ici dans sa version la plus aisée à comprendre (algorithme ??).
On peut aisément se demander quel peut-être l’intérêt d’un tel algorithme. Il est de deux ordres. D’une part, dans les jeux où certaines positions se présentent plusieurs fois dans l’arbre, il permet de ne pas recalculer le nœud comme indiqué précédemment. Mais son principal avantage apparait lorsqu’on l’utilise avec des fenêtres de recherche réduite, en particulier avec les algorithmes de la famille MTD(f).

On se rappelle que lors du début de l’algorithme alpha-beta, les bornes alpha et beta sont initialisées à + ∞ et − ∞. Or, dans 90% des positions, il est rare que la valeur d’une position évolue beaucoup. On peut donc initialiser les bornes alpha et beta à la valeur de la position courante ± є (ou є est une valeur bien choisie dépendant du jeu et/ou de la fonction d’évaluation). Ainsi, tous les coups dans l’algorithme alpha-beta qui seront en dehors de cette fenêtre seront immédiatement élagués. La méthode est efficace si l’hypothèse initiale est juste (c’est-à-dire qu’on ne peut effectivement pas gagner ou perdre plus de є). Si tel n’est pas le cas, on le détecte aisément car la valeur retournée est alors hors de la fenêtre initiale ]alpha , beta[. Il faut alors relancer l’algorithme en modifiant la fenêtre de recherche ; mais si l’on s’est donné la peine de stocker dans la table de transposition pour chaque position déjà exploré les informations acquises lors de la passe précédente on gagne un temps précieux en ne réexaminant pas certains nœuds.
C’est un poussant ce raisonnement à l’extrème, et en s’inspirant de l’algorithme Scout, qu’est né l’algorithme MTD(f) (algorithme ??).

Cet algorithme présente de nombreuses particularités qui le rendent particulièrement intéressant. Il emprunte en effet certains traits à la plupart des algorithmes que nous avons déjà rencontrés. Son principe est simple : il appelle autant de fois que nécessaire un alpha-beta pour construire un encadrement de la valeur de la position. Quand les deux bornes haute et basse se rencontrent, l’évaluation est terminée et la valeur de la position est connue. L’efficacité de l’algorithme vient de l’élagage violent qu’il effectue à chaque évaluation, car l’alpha-beta avec mémoire est appelé avec une fenêtre de taille 0. Il est d’autant plus efficace que la valeur du paramètre f dont dépend MTD(f) est proche de la valeur réelle de la position. On utilise donc en général comme valeur de f la valeur retourné par l’algorithme lors d’une itération précédente. Remarquons que la technique consistant à utiliser un alpha-beta avec une fenêtre de taille 0 est équivalent à la procédure TEST de l’algorithme SCOUT.
De récents travaux [PSDP96] ont montré d’autre part que MTD(+ ∞) était exactement équivalent à SSS*, c’est à dire qu’il développe les mêmes nœuds dans le même ordre, répondant en cela aux nombreuses questions qui se posaient depuis l’article fondateur de SSS*. On en déduit en particulier que SSS* est moins efficace que MTD(f) pour une valeur de f bien choisie.
Comme pour tous les programmes utilisant des techniques de recherche dans des arbres, la puissance de calcul est un facteur déterminant. Un moyen traditionnel d’augmenter cette puissance consiste à tenter de rendre l’exécution du programme parallèle, c’est-à-dire d’utiliser plusieurs machines (ou plusieurs processeurs) pour exécuter simultanément des parties du programme.
Il est clair que l’on peut aisément paralléliser un algorithme alpha-beta. En effet, il suffit de distribuer la recherche dans l’arbre sur l’ensemble des processeurs. Mais on ne peut pas le faire n’importe comment. On doit choisir entre quatre types de technique (nous retrouverons ce type de mécanisme lorsque nous parlerons de parallélisme en programmation logique) :
Dans un modèle totalement distribué, aucun processeur n’a de statut particulier. Chaque processeur choisit au départ une position à évaluer (au hasard et après un délai aléatoire différent de façon à limiter les conflits) et diffuse sur le réseau à l’intention des autres son choix. Au cours de la résolution, il diffuse également, à l’intention de tous les autres processeurs, l’ensemble des informations qui lui paraissent intéressantes (valuations alpha-beta de position par exemple). Ce type de modèle est plus fiable dans la mesure où la défaillance (ou l’absence) d’une machine est plus facilement surmontée. En revanche, il est beaucoup plus complexe à réaliser. En particulier, la gestion des conflits doit être faite avec soin : comment faire si deux processeurs se rendent compte qu’ils ont choisi la même branche ? Une méthode envisageable consiste à faire attendre chaque machine pendant une durée aléatoire, avant de leur faire choisir à nouveau une branche à évaluer. Enfin, un autre inconvénient est l’augmentation du débit des données qui va circuler sur le réseau de communications entre processeurs.
Il faut donc choisir sa stratégie en fonction des capacités des machines et du réseau dont on dispose. Examinons en détail le fonctionnement d’un système à forte granularité :
Nous avons ainsi décrit une implantation parallèle de l’algorithme alpha-beta21.
La recherche dans le domaine des algorithmes de jeu est d’une richesse et d’une vigueur assez extraordinaire et nous n’avons fait qu’effleuré le domaine. Nous n’avons en particulier pas parlé des alternatives au paradigme minimax, comme les algorithmes de type B* ou BPIP (Best Play for Imperfect Player). On peut se reporter avec profit à l’excellente thèse de Jean-Christophe Weill, qui a de plus le grand mérite d’être en Français [Wei95].
Nous nous proposons de développer en détail les différentes phases de la programmation du jeu d’Othello. La programmation d’Othello22 doit être divisée en trois phases : l’ouverture, le milieu de partie et la fin de partie. Nous allons nous intéresser successivement à ces trois différents types de jeu.
Il existe dans le jeu d’Othello un certain nombre d’ouvertures répertoriées. Il s’agit de séquences connues que l’on doit systématiquement utiliser en début de partie, sous peine de se retrouver en position inférieure. Le jeu d’Othello étant beaucoup plus jeune que le jeu d’échecs, la théorie des ouvertures est beaucoup moins développée. On ne s’intéresse à l’heure actuelle qu’à des séquences allant jusqu’à six coups maximum. D’autre part, les séquences recommandées ne sont souvent choisies que pour des raisons statistiques (on sait que, dans un championnat du monde donné, les meilleurs joueurs ont eu leurs meilleurs résultats avec une certaine séquence : c’est donc qu’il s’agit d’une bonne ouverture).
Les ouvertures ne sont pas stockées sous forme de séquence de coups, mais sous forme de positions indexées. Cela signifie que l’ordinateur ne stocke pas des séquences de positions, chaque séquence correspondant à une ouverture, mais stocke séparément chacune des positions avec le coup à jouer si cette position se rencontre à un instant donné. Pourquoi cette méthode ? Simplement pour éviter que l’ordinateur ne se perde dans une interversion de coups. Afin de retrouver rapidement une position dans l’ensemble des positions stockées, on les indexe en général par un certain nombre de clés (nombre de pions de chaque couleur…).
Cette technique a été amélioré considérablement par Michael Buro pour son programme Logistello, qui est actuellement le meilleur programme mondial. Buro utilise des techniques tout à fait originales pour améliorer en permanence la bibliothèque de son programme. On pourra se reporter avec profit à [Bur97] pour plus de détails.
Le jeu d’Othello est intéressant dans la mesure où il s’agit d’un jeu à information totale à nombre de coups précisément connus. On sait en effet que la partie se terminera au plus tard (et en général exactement) au 60ième demi-coup23. En fonction de la puissance de calcul disponible, il est possible de lancer une recherche exhaustive un certain nombre de demi-coups avant la fin (le 60ième coup). Dans ce cas, la fonction d’évaluation est extrêmement simple : il suffit de faire la différence entre son propre nombre de pions et le nombre de pions de l’adversaire. De plus, il s’agit d’une heuristique qui évalue parfaitement le caractère perdant ou gagnant de la position (évidemment !). L’algorithme de recherche est relativement original, puisque l’on considère que le plus efficace dans cet exercice est le NegaC*, un algorithme proche de MTD(f) mais pour lequel on recherche l’encadrement de la valeur de la position par bisection successive de l’intervalle [Wei95].
Cette caractéristique du jeu d’Othello explique en partie la force des programmes d’ordinateur : un humain est totalement incapable d’exécuter un calcul total sur une semblable profondeur sans commettre d’erreurs. Ainsi, un ordinateur jouant à Othello peut se retrouver dans une situation difficile une vingtaine de coups avant la fin de la partie et retourner (au propre et au figuré) complètement la position en sa faveur simplement par la force brute24.
Le milieu de partie est le royaume de l’algorithme alpha-beta et de la fonction d’évaluation. Nous allons examiner en détail la construction d’une fonction d’évaluation trés simple pour Othello. Cette fonction sera une fonction statique dans la mesure où le programme n’est pas capable d’apprentissage. Nous allons nous apercevoir que la construction de la fonction n’est pas chose complètement triviale, même si le jeu est simple et le but raisonnable (il ne s’agit pas de construire un programme champion du monde).
Tout d’abord, on tente d’attribuer à chaque case du jeu une valeur tactique. Cette valeur tactique doit représenter l’intérêt qu’a l’ordinateur à occuper une case ou, au contraire, à la laisser à son adversaire. Une fonction d’évaluation élémentaire consisterait donc à additionner les valeurs des cases que l’on possède et à soustraire la valeur des cases que possède l’adversaire. Une possibilité de valuation des cases est donnée dans la figure 1.8.
500 -150 30 10 10 30 -150 500 -150 -250 0 0 0 0 -250 -150 30 0 1 2 2 1 0 30 10 0 2 16 16 2 0 10 10 0 2 16 16 2 0 10 30 0 1 2 2 1 0 30 -150 -250 0 0 0 0 -250 -150 500 -150 30 10 10 30 -150 500
On peut rapidement justifier ce tableau en disant que la possession d’un coin est capitale, alors que les cases qui entourent le coin sont à éviter car elles donnent à l’adversaire accès au coin. La possession des cases centrales est importante, car elle augmente généralement les possibilités de jeu. Les bords sont également des points d’appui solides.
Une fois cette évaluation effectuée, il faut la corriger sur-le-champ. En effet, si nous possédons un coin, la valeur des trois cases environnantes doit être considérée comme positive puisqu’elles ne donnent plus accès au coin, qui est déjà occupé. De même, les cases du bord qui sont reliés au coin par une chaîne continue de pions de la même couleur sont beaucoup plus intéressantes car désormais imprenables. Un autre facteur important de la position à Othello est le nombre de cases libres contiguës à ses propres pions. Il faut essayer de le minimiser car plus ce nombre est petit et moins l’adversaire a, en général, de coups disponibles.
Le programme que nous venons de présenter garantit un niveau de jeu intéressant, mais est cependant très loin des meilleurs programmes d’Othello. Tous les meilleurs programmes utilisent aujourd’hui des techniques d’apprentissage qui peuvent être de plusieurs sortes. Ce type de mécanisme n’est pas nouveau, puisqu’il était déjà utilisé par Arthur Samuel [Sam59] dans son programme de jeu de dames.
La plupart des fonctions d’évaluation sont de la forme Σ citi où les ti sont les caractéristiques de la position et les ci les coefficients qui mesurent l’importance à accorder à telle ou telle caractéristique25. Au fur et à mesure de l’apprentissage, les coefficients ci doivent être modifiés de façon à enregistrer l’information acquise pendant les parties.
Comment modifier les coefficients ? Il est clair que l’on doit augmenter la valeur des coefficients qui prédisent correctement l’issue du coup et diminuer la valeur de ceux qui fournissent des informations incorrectes. Le problème dans un programme de jeu est qu’il faut être capable, après la partie, d’analyser les coups qui se sont révélés bons ou mauvais, de façon à modifier la fonction d’évaluation. On peut implanter ce mécanisme en supposant que toute séquence de coups qui a amené à une bonne situation est une bonne séquence et que les coefficients qui ont encouragé cette séquence doivent être renforcés et ceux qui tendaient à l’éviter, diminués (méthode de la carotte et du bâton). Quant à mesurer en quoi une situation est bonne, c’est facile lorsque l’on est proche de la fin de la partie (car on peut aisément faire des analyses exhaustives), mais en milieu de partie, on doit se fier à la fonction d’évaluation elle-même qui fournit, en quelque sorte, son propre feedback. Ainsi, à chaque coup, Arthur Samuel, dans son programme, comparait la valeur courante de la fonction d’évaluation Sc avec la valeur Sp affectée à cette position lors du calcul au coup précédent (soit deux demi-coups, et donc deux niveaux auparavant). Il en tirait alors les conséquences suivantes :
Il ne reste alors plus qu’à modifier les coefficients d’évaluation26.
Une autre technique classique consiste à faire jouer le programme contre une copie de lui-même avec certains coefficients de la fonction d’évaluation modifiés. Si la nouvelle copie l’emporte, alors on conserve la nouvelle valeur des coefficients, sinon on conserve l’ancienne et on essaie une autre modification.
L’apprentissage de base, consiste quant à lui à mémoriser, chaque fois que l’on effectue l’évaluation d’une position, la position ainsi que la valeur associée. Si par la suite, dans une recherche, cette même position est rencontrée, on ne tente pas de l’analyser avec la fonction d’évaluation mais on récupère la valeur stockée en mémoire, qui est évidemment plus précise puisqu’elle a elle-même été évaluée par une recherche alpha-beta profonde. L’inconvénient principal de cette méthode est qu’elle réclame de très importantes capacités de stockage.
La plupart des programmes d’Othello utilisent quand à eux un apprentissage sur des formes standards. Le principe en est simple : on estime (en simplifiant) que la valeur d’une position d’Othello ne dépend que de la structure des 4 bords, des 4 coins 3× 3 et du nombre de libertés des pions. On peut alors décider, par exemple, de stocker systématiquement tous les résultats de toutes les parties jouées, et en attribuer le mérite aux structures rencontrées sur les bords et dans les coins au cours de ces parties.
Un programme utilisant correctement de tels concepts devraient figurer dans les dix ou vingt meilleurs programmes mondiaux. Notons pour conclure que le problème de la suprématie homme/machine pour Othello a été réglé de façon à peu près définitive en 1997 où un match opposant Logistello au champion du monde humain Takeshi Murakami s’est terminé par le score sans appel de 6 à 0 pour le programme.
Les échecs sont considérés comme le jeu des Rois et surtout le Roi des jeux. Dès les débuts de l’IA, c’est sur les échecs que s’est porté l’effort le plus important et ce sont les échecs qui ont donné lieu à des luttes epiques que se sont livrés les meilleures équipes universitaires comme (hitech mené par Hans Berliner27, ou deep thought, mené par Feng-Hsiung Hsu28) devenus depuis deep blue avec le succès que l’on sait. Il faut sans doute craindre que la victoire de deep blue face à Gary Kasparov en mai 1997 n’ait des repercussions que l’on pourrait qualifier de néfastes : le plus grand défi que l’on s’était lancé (la victoire d’un programme sur le champion du monde humain dans le cadre de partie à cadence de tournoi et sur six parties) a été réalisé et il est probable que les efforts se porteront davantage dans d’autres directions. D’autre part, même si la lutte entre les plus importantes firmes commerciales restent réels, le niveau des programmes disponibles pour micro ordinateurs est maintenant tellement élevé qu’ils battent systématiquement 99% des joueurs. On accordera donc plus d’importance à la qualité de l’interface avec l’utilisateur qu’à la force pure du programme. Mais les grandes avancées liées aux échecs demeureront.
Les pères fondateurs de l’IA, Simon et Newell, menèrent, ainsi que le psychologue hollandais de Groot et le psychologue et Grand Maître soviétique Nicolaï Kroguious une analyse de la méthode de réflexion des grands champions d’échecs. Nous allons rapidement parler des résultats de ces études avant d’aborder les techniques de programmation proprement dites. Deux raisons à cela : tout d’abord les résultats mis en évidence par de Groot [Gro65] et Kroguious [Kro86] sont très intéressants car ils sont applicables à la plupart des raisonnements humains dans tous les domaines ; enfin, ces résultats n’ont en rien influencé les programmes d’échecs (du moins les meilleurs) qui utilisent des méthodes de raisonnement totalement différentes aujourd’hui, preuve qu’il est bien difficile d’appliquer des techniques humaines pour faire résoudre des problèmes à des machines.
La programmation de l’ouverture est certainement la chose la plus simple à réaliser. Les techniques à utiliser sont exactement les mêmes que pour la programmation des ouvertures pour Othello. Cependant, le nombre de positions aux échecs rend le problème un peu plus complexe. Il faut savoir que l’encyclopédie des ouvertures doit dépasser les 2000 pages.
Il s’agit plus d’un travail de bénédictin que de la réalisation exaltante d’algorithmes évolués. Notons une fois de plus la nécessité de ne pas stocker les séquences de coups, mais bien les positions en les indexant de façon correcte, afin de ne pas être trompé par une inversion de coups. Certains programmes se font encore duper. On peut aisément le vérifier avec la séquence suivante : e2e4 e7e6 g1f3 c7c5
Il suffit alors de demander à l’ordinateur le coup qu’il jouerait face à la position résultante. S’il répond immédiatement d4, c’est qu’il a reconnu l’inversion de coup qui a transformé une partie française en une sicilienne. La séquence classique pour atteindre cette position sicilienne est en effet : e4 c5 Cf3 e6. Le coup e6 en premier par le joueur noir fait au contraire croire à un ordinateur primaire que l’on va jouer une partie française, auquel cas il attend comme séquence standard : e4 e6 Cf3 d5
Ne trouvant pas cette séquence standard (c5 au lieu de d5), il est perdu s’il stocke ses ouvertures sous forme de séquences de coups et non sous forme de positions indexées, car il ne reconnaît aucune séquence standard et est incapable de reconnaître une position (sicilienne).
Une technique classique consiste, pour accélérer la recherche, à indexer la position sur le numéro du demi-coup où on peut la rencontrer. On peut, bien entendu, écrire un programme qui, connaissant les séquences d’ouverture, génère la structure de données appropriée pour faire de la reconnaissance de position, la réalisation d’une telle structure par un être humain étant réellement fastidieuse.
En fait, une technique plus efficace encore consiste à réaliser un programme qui utilise conjointement les deux méthodes : mémorisation des séquences d’ouverture pour une plus grande rapidité et mémorisation des positions pour la généralité. Il n’aurait recours à la seconde méthode que lorsque la première ne lui permettrait pas de conclure efficacement.
Hormis ces détails techniques, la programmation des ouvertures ne pose aucun problème difficile.
Les finales furent longtemps le talon d’Achille des programmes d’échecs avant de devenir un de leur point relativement fort.
Quel problème avait-on à résoudre ? Les ordinateurs sont efficaces en milieu de partie en raison de leur formidable habileté tactique, liée à leur grande capacité de calcul et à leurs algorithmes de recherche efficaces. Mais dans une finale, la capacité à calculer doit être bien différente. Prenons un exemple trivial. Si nous sommes dans une finale Roi et pion contre Roi et pion, et que la disposition des pièces est la suivante : pion blanc en a2, Roi noir en g4, pion noir en h2, Roi blanc en h1 avec trait au blanc (figure
La partie peut être considéré comme terminée. En effet, le Roi noir ne peut empêcher le pion blanc d’aller à Dame en a8 et le pion noir en h2 ne peut aller à Dame, bloqué qu’il est par le Roi blanc en h1. C’est l’analyse que réalise immédiatement tout joueur, même débutant. Le bon coup est évidemment a4. Mais un ordinateur raisonnant avec un algorithme alpha-beta à profondeur fixe va considérer les choses différemment. Tout d’abord, il voit qu’il peut prendre le pion h2 sur le champ, et qu’en revanche s’il ne le prend pas, il ne pourra pas le prendre au coup suivant si les noirs jouent Th3, il y a donc manque à gagner. D’autre part, il lui faudrait analyser la position à 10 demi-coups de profondeur pour s’apercevoir que le pion blanc ne peut aller à Dame que s’il est avancé sur le champ. Cette profondeur étant déraisonnable pour beaucoup d’ordinateurs, il sera aveuglé par sa gloutonnerie et jouera |Rxh2|, la partie se terminant alors par une nulle (le Roi noir capturera le pion blanc sans difficulté au bout de 10 demi-coups). Cet exemple nous montre la nécessité d’inclure dans le programme des règles particulières permettant de déterminer aisément la valeur d’un pion dans une finale sans être contraint à des analyses en profondeur trop importantes.
Un autre exemple typique de problème de finales est le suivant. On considère la position : Roi noir en f6, pion noir en g6, Roi blanc en g2, Fou blanc en f5 Cavalier blanc en g5 et Fou blanc en h1 (figure 1.10).
Le programme ne peut défendre simultanément son Fou en f5 et son Cavalier en g5. Il jouera donc |Fxg6|, gagnant un pion avant de perdre le Fou. Il se retrouve alors à jouer une finale Roi, Fou, Cavalier contre Roi qui est gagnante. Jusque-là pas d’erreur. Remplaçons maintenant le Fou blanc en h1 par un Cavalier blanc(figure 1.11).
Le problème est apparemment inchangé, la meilleure solution semble encore de jouer |Fxg6| pour gagner un pion avant de perdre une pièce. C’est d’ailleurs ce que font tous les programmes de l’ancienne génération et nombre de joueurs d’échecs novices. Il s’agit pourtant d’une erreur grave. En effet, la finale Roi, Cavalier, Cavalier contre Roi est toujours nulle. Le coup correct ici est |Fd3|, pour sauver le Fou. Après |Rxg5|, les blancs élimineront sans difficulté le pion noir restant avec leur coalition Roi, Fou, Cavalier puis materont le Roi noir. Mais là encore, il faut savoir sacrifier le court terme pour le long terme et surtout il faut savoir reconnaître certains types de positions particulières.
Signalons un dernier point capital dans beaucoup de finales : la nécessité d’établir un plan. Considérons la position suivante : Roi noir en e4, Roi blanc en g7, Fou blanc en h8, Cavalier blanc en g8 (figure 1.12).
Il s’agit d’une typique finale Roi, Fou, Cavalier contre Roi. Cette finale est gagnante. Encore faut-il mater en moins de 50 coups29. Nombre de joueurs de club ont échoué dans une semblable finale et tous les programmes de l’ancienne génération échouaient également. Le mat ne peut être atteint que par un jeu précis et un plan parfaitement établi. Un problème encore plus difficile est posé par la finale Roi, Cavalier, Cavalier contre Roi et Pion qui peut être gagné dans certains cas30. Mais la réalisation du mat en 50 coups est excessivement difficile sans plan précis.
Nous avons donc vu la nécessité d’introduire trois éléments fondamentalement nouveaux dans les programmes de finale :
Les progrès réalisés ces cinq dernières années par les programmes en résolution de finales sont extrêmement spectaculaires31. Tous les exemples que nous avons présentés ci-dessus sont maintenant résolus par des programmes que l’on peut trouver dans le domaine public sur internet. Deux facteurs ont largement contribué à la progression des ordinateurs dans les finales : les tables de transposition (que nous avons déjà présentées), et l’analyse rétrograde que nous allons maintenant détailler.
Il s’agit d’une méthode permettant de constituer des base de données indiquant à l’ordinateur quel est le coup à jouer dans une position donnée pour arriver au gain de la façon la plus rapide. La constitution de semblables bases s’est beaucoup développée dans les dix dernières années. Ainsi, il existe une base de données permettant de jouer parfaitement des finales comme (Roi + Cavalier + Fou) contre (Roi + Cavalier), une finale que même un champion du monde aurait des difficultés à gagner32.
Pour construire de semblables bases de données, les ordinateurs utilisent une méthode appelée analyse rétrograde. Prenons comme exemple la finale (Roi + Dame) contre (Roi). Il existe, si on néglige les symétries, 64× 64 × 64=262144 positions de départ. Certaines de ces positions sont impossibles (les deux Rois adjacents par exemple) : elles sont éliminées. Dans les positions restantes, on recherche celles où les noirs sont mats : ce sont les positions où le Roi noir est déjà en échec et où aucun des coups dont il dispose ne permet de le soustraire à cet échec. À partir de là, on détermine aisément les positions de mat en un coup. Ce sont les positions qui permettent au blanc d’atteindre en un coup une position de mat. On peut ainsi déterminer récursivement les positions de mat en n+1 coups à partir des positions de mat en n coups.
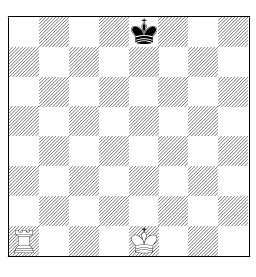
La constitution de bases de données de ce type est une technique bien particulière, relativement éloignée de la programmation classique des jeux, mais fort intéressante. Les problèmes à 5 pièces (sans pion) ont été exhaustivement résolus33, et l’on travaille activement sur les problèmes à 6 pièces. En Octobre 1991, Larry Stiller (avec l’aide de Noam Elkies et Burton Wendroff) a construit la plus longue finale gagnante connue à ce jour. La position initiale est représentée sur la figure 1.13. La résolution complète demande 223 coups. Il est clair que ce type de finale est inaccessible à l’être humain. La question est de savoir si les règles doivent être modifiées pour en tenir compte.
Nous allons retrouver les deux grands protagonistes du milieu de partie : la fonction d’évaluation et l’algorithme alpha-beta. Mais nous introduirons également quelques techniques spécifiques ou, en tout cas, surtout utilisées pour les échecs.
La fonction d’évaluation aux échecs est extrêmement complexe. La base d’une fonction d’évaluation est la valeur accordée aux pièces. On peut dire que les valeurs que la plupart des programmes accordent aux pièces sont les suivantes :
| Dame | : | 9 |
| Tour | : | 5 |
| Fou | : | 3 |
| Cavalier | : | 3 |
| Pion | : | 1 |
Il reste maintenant à raffiner la fonction d’évaluation. Tout un ensemble de paramètres interviennent. En voici quelques uns :
Ce n’est qu’un petit aperçu de ce que doit être une bonne fonction d’évaluation aux échecs.
Notons cependant un point capital : la notion de plan stratégique d’ensemble est absente. On peut, certes, introduire dans la fonction d’évaluation quelques éléments pseudo-stratégiques, comme l’attaque sur le roque adverse << à la baïonnette34 >>, mais cela reste très limité. Il s’agit bien là du principal défaut des programmes d’ordinateurs. Cela est particulièrement sensible lorsqu’ils passent de la séquence d’ouverture qu’ils jouent << par cœur >> au milieu de partie. En effet, à chaque ouverture est associée une idée stratégique et la suite de la partie doit développer cette idée. Ainsi une sicilienne doit être jouée de façon agressive par les blancs qui doivent attaquer rapidement le petit roque noir, alors que la chance des noirs se situe en général à l’aile dame. Or un programme est incapable de saisir ces subtilités stratégiques et appliquera la même fonction d’évaluation quelle qu’ait été l’ouverture. Tous les programmes d’ordinateur, même les meilleurs, manquent de << liant >> dans leur jeu, ce qui rend leur style facilement reconnaissable et les laisse encore vulnérables. On ne connaît actuellement aucune méthode pour remédier à cet état. Simplement, la force tactique des programmes leur permet de compenser leur faiblesse stratégique.
La technique de recherche dans l’arbre de jeu est un algorithme alpha-beta tel que nous l’avons décrit au paragraphe précédent. La technique de contrôle de temps de jeu et de reclassement des coups avant d’aborder des recherches plus profondes est également identique. Il faut cependant introduire certaines techniques indispensables aux échecs35 :
Le Fou blanc en a4 est perdu. En effet, il ne pourra échapper au pion b5 ou au pion c5 (qui va venir en c4). La séquence qui provoquera la perte du Fou est |Fb3| suivi de c4 par les noirs et le Fou est perdu. Mais un algorithme alpha-beta tente simplement de repousser cette éventualité au-delà de son horizon de recherche (d’où le nom d’effet horizon). Il va donc tenter de jouer une séquence de coups à riposte forcée qui repoussera hors de son champ de vision la séquence << déplaisante >>. Dans le cas présent, il prévoit par exemple (profondeur 5) : |1. e5,d*e5| (obligatoire car sinon le Cavalier en f6 tombe), |2.Cd5,C*d5| (on ne peut jouer |2.:b*a4| car alors |3.C*e7+|), |3.T*d5|.
Arrivé à cette position, le programme applique son mécanisme de retour à l’équilibre. Mais il ne voit rien de dangereux car après |3.:b*a4| il voit |4. T*d7| et récupère le Fou. En fait, son raisonnement est incorrect car les noirs intercalent le coup intermédiaire |Fe6| et le jeu se poursuit en fait par : |3.:Fe6; 4.Fb3,c4| et le Fou est perdu.
Le programme, pour trouver la solution correcte, devrait effectuer la recherche à la profondeur 7, ce qui est prohibitif pour un ordinateur moyen. Certains écrivaient, il y a quelques années, que ce type de situation était ingérable par un ordinateur. En fait, la plupart des bons programmes de jeu utilisent aujourd’hui une technique appelée recherche secondaire qui leur permet de trouver la solution du problème précédent en quelques secondes. Il s’agit simplement de relancer la recherche alpha-beta à une profondeur supérieure, mais uniquement sur la branche (voire uniquement sur la position terminale de la branche) qui contient le coup sélectionné. Il s’agit, en quelque sorte, d’une vérification de la validité du coup choisi. Comme l’évaluation n’est faite que sur la position terminale sélectionnée, le temps nécessaire est raisonnable. Certes, ce mécanisme ne permet pas de faire disparaître l’effet horizon, mais il en limite considérablement les effets36.
Avec l’algorithme SEX, on utilise une variable SX qui prend une valeur nettement plus grande que la profondeur à laquelle on veut chercher (une valeur typique est dix fois la profondeur, si n vaut 3, SX vaut 30), mais à chaque descente d’un niveau dans l’arbre, on diminue SX d’une quantité variable en fonction de l’intérêt du coup joué. Ainsi, un coup << moyen >> soustrait 10 à SX, une prise ou un échec est un coup intéressant, et on diminue peu SX (2 ou 3) ; en revanche, une retraite de pièces est un coup peu intéressant et on diminue beaucoup SX (jusqu’à 35). La recherche est terminée quand SX devient négatif ou nul.
De cette façon, les coups intéressants sont étudiés de façon plus profonde, et les coups << peu intéressants >> sont rapidement abandonnés.
Signalons, pour conclure, un des inconvénients de la méthode minimax. Si l’ordinateur se trouve dans une situation perdante et qu’il a le choix entre deux coups, dont le second est légèrement plus mauvais que le premier mais tend un piège à l’adversaire, il sera incapable de s’en apercevoir. Le principe minimax choisira obligatoirement le premier, alors qu’il garantit presque assurément la perte de la partie, alors qu’un joueur humain tentera le tout pour le tout et jouera le second coup. La notion de piège est bien difficile à formaliser, cependant Donald Michie proposa, il y a quelques années, une intéressante méthode qu’il est bon de rapporter. Supposons que nous ayons un arbre à deux niveaux que nous parcourons par une méthode minimax. L’ordinateur cherche la valeur S1 du premier coup de niveau 1. À partir de la position P1 correspondant à ce coup, son adversaire peut atteindre trois positions P11, P12 et P13 dont les scores sont respectivement S11, S12, S13. Théoriquement, l’ordinateur devrait remonter comme valeur au niveau 1 le minimum de ces trois valeurs. Michie propose de raffiner la méthode en prenant comme valeur du niveau 1 non pas le minimum, mais la combinaison linéaire :
| p11 × S11+ p12 × S12 + p13 × S13 |
p11, p12, p13 représentent les probabilités que l’adversaire a de jouer les coups S11, S12, S13 d’après l’ordinateur.
Comment évaluer ces probabilités ? Michie a mis au point une méthode pour les échecs, qu’il appelle modèle de discernement. Il estime que le discernement d’un joueur face à une position donnée est donné par la formule empirique :
| d= (C/1000 +1) 31/(n+0.01) |
C représente le classement ELO38 du joueur que l’on affronte et n le nombre de coups dont on a calculé une valuation. Pourquoi cette formule ? Il est clair qu’un joueur joue d’autant mieux qu’il est plus fort. D’autre part, nous savons que plus il y a de coups différents possibles et plus le choix est difficile, surtout s’ils ont des valeurs proches. Michie estime alors que la probabilité qu’un joueur de discernement d face à une position joue un coup menant à un score estimé v sera :
| p = A dv |
où A est un coefficient bien choisi pour normer la probabilité. Il serait intéressant de tester la méthode de Michie, mais aucun programme ne semble l’utiliser aujourd’hui.
Enfin, et d’après39 Feng-Hsiung Hsu (responsable du projet deep thought), les programmes d’échecs à l’heure actuelle n’utilisent pas de technique d’apprentissage40 :
<< Une grave erreur doit être évitée : deep thought n’apprend pas. La fonction d’évaluation que nous utilisons est linéaire par rapport à presque tous ses termes (de 100 à 150). Nous ne faisons qu’une optimisation du modèle de mérite dans un espace multi-dimensionnel, en utilisant un mécanisme de régression linéaire. Ce processus produit des résultats intéressants, même s’il n’est pas clair qu’il produise toujours les effets désirés. >>
Pour plus d’informations sur les programmes qui jouent aux échecs, on ne peut que conseiller [LN91, MS90].
Notre exposé sur la programmation du bridge sera moins détaillé et moins complet que celui consacré aux échecs. La raison en est simple : peu de gens se sont intéressés à la programmation du bridge. On peut penser que la raison de ce désintérêt est l’aspect << chance >> qui existe au bridge. Les gens pensent que si un programme d’échecs l’emporte, il est meilleur, alors qu’un programme de bridge peut simplement << avoir de la chance >>. Il y a également le facteur << convivialité >> du bridge : on ne joue aux échecs qu’avec un partenaire, alors que le bridge se joue à quatre et on joue souvent au bridge plus pour être entre amis que pour améliorer son niveau de jeu. Enfin, une raison technique est que la réalisation d’un programme, même élémentaire, est beaucoup plus difficile qu’aux échecs : il faut en effet écrire un programme d’annonces correct, ce qui n’est déjà pas simple, puis introduire, au lieu des mécanismes de recherche classiques, des analyses probabilistes portant à la fois sur les informations fournies par les annonces et sur les informations fournies par le jeu de la carte. Il faut également utiliser des notions de planification pour choisir, avant de commencer le jeu de la carte (du moins pour le camp déclarant), la façon dont on estime pouvoir réaliser son contrat. En fait, tous les jeux à information incomplète sont difficiles à programmer, car il est impossible d’utiliser directement des méthodes de recherche classiques, en raison du très important nombre de distributions possibles de mains.
Le premier problème qui se pose au bridge est de construire un programme d’annonces efficace. Les annonces au bridge sont quelque chose de complexe et de très codifié. On pourrait penser qu’il est raisonnable de créer un système capable de contenir l’ensemble des situations possibles. C’est en fait irréalisable. Il faut donc construire un système à mi-chemin entre le << par cœur >> et des mécanismes heuristiques plus généraux. Un exemple typique de la difficulté de la programmation des enchères au bridge est le suivant : Nord annonce 1♠. Cela signifie qu’il a entre 13 et 20 points distribution-honneurs41 et au moins cinq Piques. Il attend alors la réponse de son partenaire Sud. Les réponses de Sud sont également codifiées de façon très précise comme l’est la première enchère. Mais supposons qu’Est intervienne entre Nord et Sud. Voilà Sud dans une situation bien difficile. Il devra moduler sa réponse en fonction de l’intervention d’Est. Si Est a simplement dit 1SA42, il pourra reparler au niveau de 2 et ne sera privé que de l’enchère de 1SA. En revanche, si Est a fait une enchère de barrage au niveau de 4, le problème est bien différent.
Le problème des enchères est encore compliqué par le fait qu’il existe plusieurs systèmes d’enchères différents, ainsi que des conventions spéciales que le programme doit également connaître.
Enfin, un bon programme doit également savoir utiliser les informations que donnent les enchères pour mettre à jour les probabilités de présence des cartes chez les autres joueurs. Ainsi, supposons qu’un des adversaires ouvre de 1♠. Nous savons qu’il a entre 12 et 20 points d’honneur43 et au moins cinq Piques. Nous pouvons donc modifier les probabilités de présence des cartes dans sa main. Jusque-là, pour toute carte que nous ne possédions pas, nous pouvions supposer que chacun des autres joueurs avait une probabilité de 1/3 de la posséder. Si je possède moi-même 10 points d’honneur, il en reste 30 dans le jeu. Le joueur qui a ouvert doit avoir en moyenne 13 points d’honneur44, donc je dois désormais donner à chacun des honneurs qu’il peut avoir dans sa main, une probabilité de 13/30=0.43. Nous devons, en conséquence, modifier la probabilité de présence de ces mêmes cartes dans toutes les autres mains. Le processus doit se poursuivre tout au long des enchères. À la fin, un bon programme doit avoir accumulé suffisamment d’informations pour pouvoir planifier correctement son jeu.
Le jeu de la carte est excessivement difficile à programmer. Il faut en effet planifier le jeu avant l’entame, modifier les plans en cours de partie si les défendants ne suivent pas la ligne prévue ou que les cartes ont une distribution défavorable, déclencher une recherche exhaustive quand la position de l’ensemble des cartes est connue ou quand le nombre de distributions possibles est réduit, et modifier en permanence les probabilités de présence des cartes dans les autres mains en fonction des renseignements que donnent les cartes jouées.
Considérons ce dernier point sur un exemple, pour bien montrer comment réaliser les modifications de probabilité. Supposons que l’ordinateur (en Nord) est le déclarant, qu’il a la main et décide de jouer le 4 de Pique alors que les Piques qu’il connaît sont répartis de la façon suivante (Pique n’a pas encore été joué, et comme Nord est le déclarant, Sud est le mort) :
Supposons qu’Est fournisse le 5, Sud le 9, qu’Ouest fasse le pli avec la Dame de Pique. Quelles informations pouvons-nous en retirer ? Sur Est peu de chose ; en revanche, nous pouvons améliorer nos connaissances sur Ouest. Comme nous possédons le Roi et l’As, nous savons qu’Ouest devait jouer le 10, le Valet ou la Dame pour réaliser la levée. S’il avait eu la Dame et le 10 sans le Valet, il aurait certainement joué le 10. Donc, nous savons qu’il a une des trois45 distributions suivantes : (Dame, Valet, 10) ou (Dame, Valet) ou (Dame). Si nous ne disposons d’aucune information venant de l’ouverture concernant Pique, nous pensons que chaque carte non localisée a une chance sur deux de se trouver en Ouest. Donc la probabilité de chaque distribution est :
| Dame,Valet,10 : | 0.5 × 0.5 × 0.5 | =0.125 |
| Dame,Valet : | 0.5 × 0.5 × (1−0.5) | =0.125 |
| Dame : | 0.5 × (1−0.5) × (1−0.5) | =0.125 |
D’après le théorème de Bayes, nous savons que la probabilité que la Dame provienne d’une de ces distributions est :
| Dame,Valet,10 : | 0.125/(0.125+0.125+0.125) | =1/3 |
| Dame,Valet : | 0.125/(0.125+0.125+0.125) | =1/3 |
| Dame : | 0.125/(0.125+0.125+0.125) | =1/3 |
D’après ces résultats, nous voyons que la probabilité qu’Ouest ait le 10 est 0.33 et celle qu’il ait le Valet de 0.67. Nous devons donc ajuster les probabilités dans le jeu d’Ouest ainsi que dans le jeu d’Est. Nous venons de voir, sur cet exemple, que le re-calcul des probabilités n’est pas chose totalement triviale, même sur un cas simple.
Il nous reste maintenant à examiner comment jouer effectivement. À partir du moment où nous avons localisé l’intégralité des cartes, ou tout au moins que nous n’avons plus qu’un nombre de distributions possibles réduit, nous pouvons lancer une recherche exhaustive sur l’arbre de jeux. La fonction d’évaluation devra prendre en compte, non pas uniquement le nombre de plis faits, mais également le gain ou la perte au score. Il faudra aussi, dans certains cas, ne pas hésiter à utiliser la méthode de Michie telle que nous l’avons décrite, si, par exemple, nous devons, pour réaliser notre contrat, compter sur une faute adverse.
En début de partie, il faudra, si l’on est le déclarant, établir un plan de jeu. Réaliser un plan de jeu passable est relativement simple, on peut par exemple utiliser l’algorithme suivant :
Il est bien évident qu’un semblable algorithme serait complètement insuffisant pour réaliser un programme véritablement fort.
En ce qui concerne le jeu << au jour le jour >>, on peut implanter un certain nombre d’heuristiques classiques :
Ces heuristiques ne permettront pas de réaliser un programme très fort mais doivent suffire à écrire un programme médiocre. On doit également utiliser les probabilités de répartition des cartes lorsque cela est possible.
Il existe bien d’autres heuristiques que l’on peut implanter, mais on ne possède que peu de résultats sur leur efficacité. Il existe quelques machines commerciales disponibles, mais elles sont toutes très faibles, même pas du niveau d’un joueur de club moyen.
D’autres jeux ont été programmés avec plus ou moins de succès :
Le tournoi se déroulait en huit matches de quatre parties chacun. chinook en gagna quatre, fit quatre nulles et termina ainsi second du tournoi derrière Tinsley (+5, =3, -0). Le match contre Tinsley se termina par une nulle (+0, =4, -0). chinook est ainsi le premier ordinateur à se qualifier pour une finale officielle de championnat du monde. La fédération américaine ayant refusé que le programme soit désigné comme challenger officiel, Tinsley a abandonné son titre et a affronté chinook dans un match qui pouvait être considéré comme un championnat du monde officieux, à Londres, au mois d’août 1992. Tinsley l’emporta au terme des 40 parties sur le score de 4 parties gagnées, 2 parties perdues et 34 parties nulles, une performance remarquable pour chinook. Un match revanche eut lieu en 1994, qui vit la victoire de chinook par abandon, Marion Tinsley étant déjà affaibli par la maladie qui devait l’emporter. Depuis, chinook a affronté le successeur de Tinsley, Don Lafferty, et a successivement annulé le premier match en 1994 et gagné le second en 1995. Il faut noter que la fédération de checkers autorise désormais chinook à participer à la majorité des grands tournois, et a créé un titre spécial de champion du monde homme-machine qui sansctionne le vainqueur du match opposant le champion du monde humain au meilleur programme.
Les principes généraux pour la programmation du jeu de Checkers sont les mêmes que pour le jeu d’échecs avec quelques différences notables :
Les gens intéressés par chinook et la programmation des dames américaines peuvent se reporter aux excellents articles de Jonathan Schaeffer [Sch89a, Sch89b, SCT+91, Sch91, SCT+92].
Jonathan Schaeffer estime que, dans l’état actuel de la technologie, il doit être possible de résoudre complètement le jeu de checkers [SCT+92], c’est-à-dire de construire un programme capable de jouer parfaitement de façon certaine. Si l’équipe de chinook y parvient, les checkers seront le premier jeu réellement complexe48 à être résolu.
Dans un programme de Go, il y a trois parties principales : les structures qui représentent la connaissance, la fonction d’évaluation pour déterminer le score et la fonction de sélection des coups.
Cette rapide description montre bien que l’approche de la programmation du Go se distingue très nettement de celle des autres jeux. Elle s’appuie plus sur des considérations expertes que sur des considérations de force brute. Il reste à savoir quel sera l’avenir de ces programmes. Les premiers programmes d’échecs étaient eux aussi des programmes plus orientés vers l’expertise que vers la force, et la tendance s’est lentement inversée.
Le téléchargement ou la reproduction des documents et photographies
présents sur ce site sont autorisés à condition que leur origine soit
explicitement mentionnée et que leur utilisation
se limite à des fins non commerciales, notamment de recherche,
d'éducation et d'enseignement.
Tous droits réservés.
Dernière modification: 09:48, 22/02/2024